Life-Like Hexagonal Cellular Automata
20 Sep 2016
There are two “neighborhoods” often used in cellular automata, the Von Neumann neighborhood of 4 cells and the Moore neighborhood of 8 cells. Conway’s Game of Life uses the Moore neighborhood. One can also used a neighborhood of 6 cells on a skewed grid to implement a hexagonal cellular automata. Hexagonal cellular automata don’t seem to be quite as rich as the Game of Life, but still produce some interesting patterns. One produces a maze of twisty little passages, all alike:
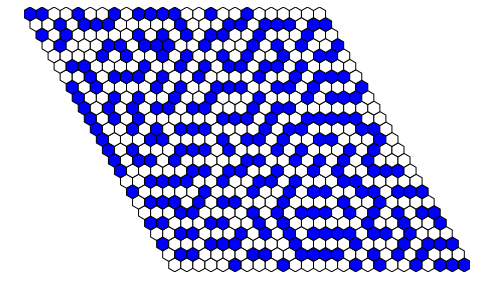
Here’s a Jupyter Notebook implementing Life-like cellular automata on a hex grid. To use it interactively, download it to your local machine.
Related Posts
- 2023-11-04: Spherical area coordinates, and a derived triangle center
- 2023-07-29: Homogeneous coordinates on the sphere with vectors
- 2022-08-30: Scaling the Schwarz triangle function
- 2022-08-27: Edges in the image of the Schwarz triangle function
- 2022-07-20: Area-preserving swirling of the disk
- 2022-03-03: Some dubious ways to calculate conformal polyhedral projections
- 2021-10-02: A variation on the Chamberlin trimetric map projection
- 2021-08-31: Snyder's equal-area projection
- 2021-06-12: Perspective projections with vectors
- 2021-05-29: A (sort of) Euclidean triangle on a non-Euclidean surface